1.1.3: Making Scaled Copies

Lesson

Let's draw scaled copies.
  1. The value of \(25\cdot (8.5)\) is:
    1. More than 205
    2. Less than 205
    1. More than 10
    2. Less than 10
    1. More than 0.2
    2. Less than 0.2

    Exercise \(\PageIndex\): Drawing Scaled Copies

    clipboard_eaa2040aa3fbd68cf96a837b6ab3e3c7d.png

    1. Draw a scaled copy of either Figure A or B using a scale factor of \(3\).
    2. Draw a scaled copy of either Figure C or D using a scale factor of \(\frac\).

    Exercise \(\PageIndex\): Which Operations? (Part 1)

    Diego and Jada want to scale this polygon so the side that corresponds to 15 units in the original is 5 units in the scaled copy.

    clipboard_ecf61ffd17673a7acab0d2954e8035289.png

    Diego and Jada each use a different operation to find the new side lengths. Here are their finished drawings.

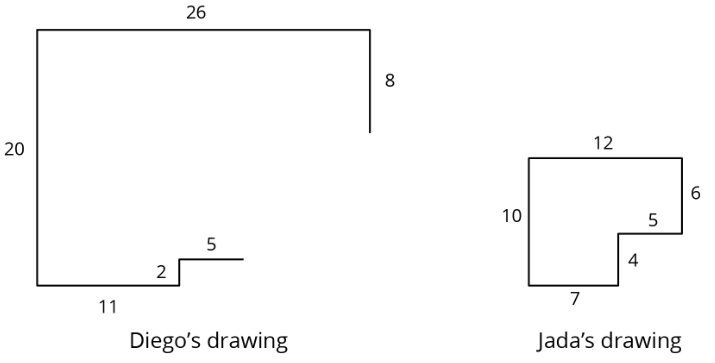
    clipboard_e8c99a8e7886ffb34d96574a8d7c38f9e.png

    1. What operation do you think Diego used to calculate the lengths for his drawing?
    2. What operation do you think Jada used to calculate the lengths for her drawing?
    3. Did each method produce a scaled copy of the polygon? Explain your reasoning.

    Exercise \(\PageIndex\): Which Operations? (Part 2)

    Andre wants to make a scaled copy of Jada's drawing so the side that corresponds to 4 units in Jada’s polygon is 8 units in his scaled copy.

    clipboard_edf4221b66671dfd846bdd383893e1e63.png

    1. Andre says “I wonder if I should add 4 units to the lengths of all of the segments?” What would you say in response to Andre? Explain or show your reasoning.
    2. Create the scaled copy that Andre wants. If you get stuck, consider using the edge of an index card or paper to measure the lengths needed to draw the copy.

    Are you ready for more?

    The side lengths of Triangle B are all 5 more than the side lengths of Triangle A. Can Triangle B be a scaled copy of Triangle A? Explain your reasoning.

    Summary

    Creating a scaled copy involves multiplying the lengths in the original figure by a scale factor.

    For example, to make a scaled copy of triangle \(ABC\) where the base is 8 units, we would use a scale factor of 4. This means multiplying all the side lengths by 4, so in triangle \(DEF\), each side is 4 times as long as the corresponding side in triangle \(ABC\).

    clipboard_ecf8e710ef213fe0548db9ed0ffc6e270.png

    Glossary Entries

    When part of an original figure matches up with part of a copy, we call them corresponding parts. These could be points, segments, angles, or distances.

    For example, point \(B\) in the first triangle corresponds to point \(E\) in the second triangle. Segment \(AC\) corresponds to segment \(DF\).

    clipboard_e2728b3247bf3bb939a001aa3dc3bac53.png

    Definition: Scale Factor

    To create a scaled copy, we multiply all the lengths in the original figure by the same number. This number is called the scale factor.

    In this example, the scale factor is 1.5, because \(4\cdot (1.5)=6\), \(5\cdot (1.5)=7.5\), and \(6\cdot (1.5)=9\).

    clipboard_e919f0ad3848582ce451f8d8df95d9f1e.png

    Definition: Scaled Copy

    A scaled copy is a copy of an figure where every length in the original figure is multiplied by the same number.

    For example, triangle \(DEF\) is a scaled copy of triangle \(ABC\). Each side length on triangle \(ABC\) was multiplied by 1.5 to get the corresponding side length on triangle \(DEF\).

    clipboard_e7a834304f2fbd754976975695baf4ec5.png

    Practice

    Here are 3 polygons.

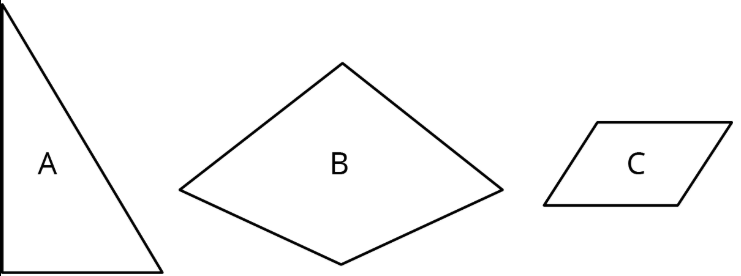
    clipboard_e1f45142655ce47692b68319789d966fc.png

    Draw a scaled copy of Polygon A using a scale factor of 2.

    Draw a scaled copy of Polygon B using a scale factor of \(\frac\).

    Draw a scaled copy of Polygon C using a scale factor of \(\frac\).

    Quadrilateral A has side lengths 6, 9, 9, and 12. Quadrilateral B is a scaled copy of Quadrilateral A, with its shortest side of length 2. What is the perimeter of Quadrilateral B?

    Here is a polygon on a grid.

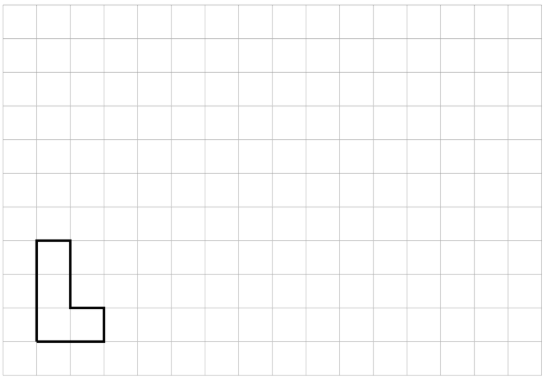
    clipboard_e691b8f2acf02260a76910c3f68418409.png

    Draw a scaled copy of this polygon that has a perimeter of 30 units. What is the scale factor? Explain how you know.

    Priya and Tyler are discussing the figures shown below. Priya thinks that B, C, and D are scaled copies of A. Tyler says B and D are scaled copies of A. Do you agree with Priya, or do you agree with Tyler? Explain your reasoning.

    clipboard_ea6d9cc1ff71c43a90f777b5816a9425f.png

    This page titled 1.1.3: Making Scaled Copies is shared under a CC BY license and was authored, remixed, and/or curated by Illustrative Mathematics.

    1. Back to top
      • 1.1.2: Corresponding Parts and Scale Factors
      • 1.1.4: Scaled Relationships